Optimizing hybrid network topologies in communication networks through irregularity strength
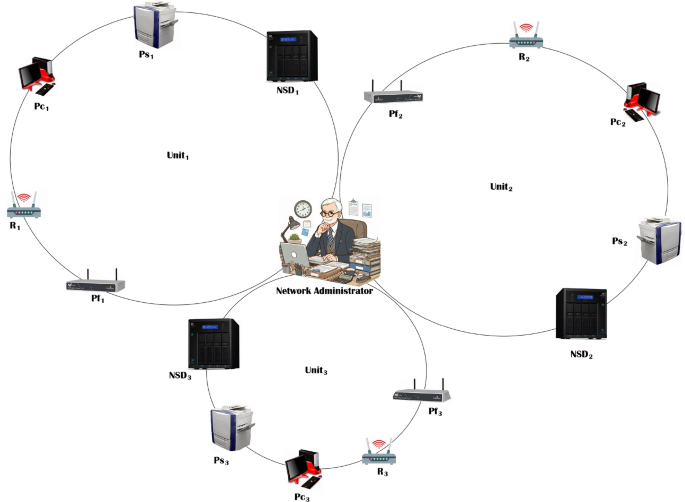
Corona product of two graphs \(C_{p}\) and \(P_m\) is denoted as \(C_{p}\odot P_m\). It is basically a graph operation which combines \(C_{p}\) and \(P_m\) in a unique way. There are three steps to perform this operation: Firstly, a copy of \(C_{p}\) and number of copies of \(P_m\) equivalent to the vertex set of given graph \(C_{p}\) are considered. In next step, each vertex \(v_i\) of \(C_{p}\) is joined to the each vertex in the i-th copy of \(P_m\). Finally, after this operation a new graph is generated that has structure of \(C_{p}\) with each of its vertices expanded into a copy of \(P_m\) attached to it. In this paper, there is a brief study of edge, vertex and total labeling of a generalized model for the \(C_{p}\odot P_m\) and the exact solutions are investigated with the help of certain parameters. For the exact solutions that admits \(C_{p}\)-covering with respect to edge, vertex and total labeling Lemmas 4, 5, 6 play a vital role. After defining these lemmas, \(C_p\)-irregularity strength of \(C_{p}\odot P_m\) will be calculated.
Lemma 4 establishes lower bounds for edge \(C_{3}\)-irregularity strength.
Lemma 4
Let \(C_{3}\odot P_m\) graph admitting the \(C_{3}\)–covering given by t sub-graphs isomorphic to \(C_3\). Then
$$\mathrm{{ehs}}(C_{3}\odot P_m,C_{3})\ge \Big \lceil 1+\frac{t-1}{|E(C_{3})|} \Big \rceil .$$
The Lemma 5 establishes the lower bounds for the vertex \(C_{3}\)-irregularity strength.
Lemma 5
Let \(C_{3}\odot P_m\) graph admitting the \(C_{3}\)–covering given by t sub-graphs isomorphic to \(C_3\). Then
$$\mathrm{{vhs}}(C_{3}\odot P_m,C_{3})\ge \Big \lceil 1+\frac{t-1}{|V(C_{3})|} \Big \rceil .$$
The lower bounds of total \(C_{3}\)-irregularity strength are given by Lemma 6.
Lemma 6
Let \(C_{3}\odot P_m\) graph admitting the \(C_{3}\)–covering given by t sub-graphs isomorphic to \(C_3\). Then
$$\begin{aligned} ths (C_{3}\odot P_m,C_{3})\ge \Big \lceil 1+ \frac{t-1}{ \mid V(C_{3}) \mid + \mid E(C_{3})\mid } \Big \rceil . \end{aligned}$$
Total \(C_{3}^{\Re (j)}\)-irregularity strength of corona product of \(C_{3}^{\Re (j)}\) with path graph
In “Introduction”, detailed construction of \(C_{3}\odot P_m\) has been provided. Isomorphic \(C_3\) covering generates a family of subgraphs written as \(C_{3}^{\Re (j)} = (C_{3}^{\Re (1)}, C_{3}^{\Re (2)}, C_{3}^{\Re (3)},\dots , C_{3}^{\Re (t)})\), here \(\Re (i)=i\) is a function to distinguish total covering. Total \(C_{3}^{\Re (j)}\)-weight for one of the given \(C_{3}^{\Re (j)}\), \(j = 1, 2,\dots , t\) is the sum of each labeled vertex and edge in the provided \(C_{3}^{\Re (j)}\). Total \(C_{3}^{\Re (j)}\)-weight labeling for an arbitrary \(C_{3}^{\Re (j)}\) is defined as, \(wt_{\gamma }(C_{3}^{\Re (j)})=\sum _{v\in V ( C_{3}^{\Re (j)})} \gamma (v) + \sum _{e\in E(C_{3}^{\Re (j)})} \gamma (e).\) Here \(\gamma\) specifies the total \(C_{3}^{\Re (j)}\)-labeling for the subgraph such that \(C_{3}^{\Re (j)} \subseteq C_{3}\odot P_m\). For total \(C_{3}^{\Re (j)}\)-irregularity strength each \(C_{3}^{\Re (j)}\)-weight has a different weights in \(C_{3}^{\Re (j)}\) and satisfy \(wt_{\gamma }(C_{3}^{\Re (j)})\ne wt_{\gamma }(C_{3}^{\Re (j+1)})\), here \(1 \le j \le t\). This condition proves total \(C_{3}^{\Re (j)}\)-irregular \(C_{3}^{\Re (j)}\)-labeling in \(C_{3}\odot P_m\). Total irregularity strength exists if there exist a least positive integer k for which total irregular labeling is possible. Forthwith, \(C_{3}^{\Re (j)}\)-irregularity under \(C_{3}^{\Re (j)}\)-labeling is expressed as \(ths(C_{3}\odot P_m, C_{3})\). Symbol of \(ths(C_{3}\odot P_m,C_{3})\) is defined first time in41.
Now we are going to calculate \(ths(C_{3}\odot P_m, C_{3})\) for the generalized structure of \(C_{3}\odot P_m\) under \(C_{3}^{\Re (j)}\)-labeling with the help of Lemma 6.
Theorem 4
Let \(C_{3}\odot P_m\) be the corona product of cycle graph and path graph \(P_m\). The graph \(C_{3}\odot P_m\) is admitting \(C_{3}-covering\) generating a family of \(~3\sigma -2\) isomorphic copies of \(C_{3}^{\Re (j)}\) as \(\left( C_{3}^{\Re (1)}, C_{3}^{\Re (2)}, C_{3}^{\Re (3)},\dots , C_{3}^{\Re (3\sigma -2)}\right)\) with a parameter \(3 \le \sigma\). Then
$$\mathrm{{ths}}(C_{3}\odot P_m, C_{3}) = \Big \lceil \frac{\sigma +1}{2}\Big \rceil .$$
Proof
Consider \(C_{3}\odot P_m (x, y, z, u_{i}, w_{i}, w_{i})\) be a \(C_{3}\odot P_m\) for a positive integer \(3 \le \sigma\). \(C_{3}\odot P_m\) has order \(3(m +2)\) and size \(6(m +1)\) such that \(k \le ths(C_{3}\odot P_m)\) for the all following cases, where k is the least positive integer for which \(C_{3}\odot P_m\) admitting \(C_{3}^{\Re (j)}\)-irregular total \(C_{3}^{\Re (j)}\)-labeling.
The vertex set and the edge set of \(C_{3}\odot P_m\) are defined as follows:
$$V(C_{3}\odot P_m) = \{x,y,z\} \cup \{u_i,v_i,w_i: 1\le i \le \frac{ \sigma +1}{2} \},$$
and
$$E(C_{3}\odot P_m) = \{xu,xv,xw,yu,yv,yw,zu,zv,zw,\} \cup \{uu_i,vv_i,ww_i: 1\le i \le \frac{ \sigma +1}{2} \}.$$
Total labeling of \(C_{3}\odot P_m\) is defined as,
$$\gamma : V(C_{3}\odot P_m) \cup E(C_{3}\odot P_m)\rightarrow \{1,2,3,\ldots ,k\}$$
. The generalized solutions of total labeling in \(C_{3}\odot P_m\) for \(3 \le \sigma , 1 \le i \le \sigma -1\) are defined as,
$$\begin{aligned} \gamma (x)&=1, \\ \gamma (y)&=\Big \lceil \dfrac{\sigma +1}{2}\Big \rceil ,\\ \gamma (z)&=\Big \lceil \dfrac{\sigma +1}{2}\Big \rceil ,\\ \gamma (u_i)&=\Big \lceil \dfrac{i+3}{5}\Big \rceil ,\\ \gamma (w_{i})&= {\left\{ \begin{array}{ll} \Big \lceil \dfrac{2 i+\sigma +5}{10}\Big \rceil ,& {if \sigma = odd}\\ \\ \Big \lceil \dfrac{2i+\sigma +4}{10}\Big \rceil ,& {if \sigma = even }\\ \end{array}\right. }\\ \gamma (w_{i})&= {\left\{ \begin{array}{ll} \Big \lceil \dfrac{2i+3\sigma +5}{10}\Big \rceil ,& {if \sigma = odd} \\ \\ \Big \lceil \dfrac{2i+3\sigma +4}{10}\Big \rceil ,& {if \sigma = even}\\ \end{array}\right. }\\ \gamma (xy)&= {\left\{ \begin{array}{ll} 2\Big \lceil \dfrac{ \sigma -4}{6}\Big \rceil +1,& {if \sigma \equiv 0,1,2,5 \pmod 6} \\ \\ 2\Big \lceil \dfrac{ \sigma -2}{6}\Big \rceil +1,& {if \sigma \equiv 3,4 \pmod 6} \\ \end{array}\right. } \end{aligned}$$
$$\begin{aligned} \gamma (yz)&= {\left\{ \begin{array}{ll} 2\Big \lceil \dfrac{ \sigma -2}{6}\Big \rceil ,& {if \sigma \equiv 0,3,4,5 \pmod 6} \\ \\ 2\Big \lceil \dfrac{ \sigma -6}{6}\Big \rceil +1,& {if \sigma \equiv 1,2 \pmod 6} \\ \end{array}\right. } \\ \gamma (zx)&= {\left\{ \begin{array}{ll} 2\Big \lceil \dfrac{ \sigma -6}{6}\Big \rceil +1,& {if \sigma \equiv 1,2,3,4 \pmod 6} \\ \\ 2\Big \lceil \dfrac{ \sigma -4}{6}\Big \rceil ,& {if \sigma \equiv 0,5 \pmod 6} \\ \end{array}\right. } \\ \gamma (xu_i)&=\Big \lceil \dfrac{i+1}{5}\Big \rceil ,\\ \gamma (yv_i)&= {\left\{ \begin{array}{ll} \Big \lceil \dfrac{2i+\sigma }{10}\Big \rceil ,& {if \sigma = even}, \\ \\ \Big \lceil \dfrac{2i+\sigma +1}{10}\Big \rceil ,& {if \sigma = odd}, \end{array}\right. } \\ \gamma (zw_i)&= {\left\{ \begin{array}{ll} 1, \\ \Big \lceil \dfrac{2i+3\sigma }{10}\Big \rceil ,& {if \sigma =even}, \\ \\ \Big \lceil \dfrac{2i+3\sigma +1}{10}\Big \rceil ,& {if \sigma =odd}, \end{array}\right. } \\ \gamma (u_{i} u_{i+1})&=\Big \lceil \dfrac{i}{5}\Big \rceil ,\\ \gamma (w_{i}v{i+1})&= {\left\{ \begin{array}{ll} \Big \lceil \dfrac{2i+\sigma -2}{10}\Big \rceil ,& {if \sigma = even}, \\ \\ \Big \lceil \dfrac{2i+\sigma -1}{10}\Big \rceil ,& {if \sigma = odd}, \end{array}\right. } \\ \gamma (w_{i}w_{i+1})&= {\left\{ \begin{array}{ll} 2, \\ \Big \lceil \dfrac{2i+3\sigma -2}{10}\Big \rceil ,& {if \sigma = even}, \\ \\ \Big \lceil \dfrac{2i+3\sigma -1}{10}\Big \rceil ,& {if \sigma =odd}, \end{array}\right. } \\ \end{aligned}$$
It is easily evident that all total labels in \(C_{3}\odot P_m\) with \(C_{3}^{\Re (j)}\)-labeling are at most t. We get the following relations for \(1\le i \le \sigma -1\);
$$\begin{aligned} wt_{1}&= wt_{\gamma } (xyz) = \gamma (x)+\gamma (y)+\gamma (z)+\gamma (xy)+\gamma (yz)+\gamma (zx),&\\ wt_{2}&= wt_{\gamma } (xu_i u_{i+1}) = \gamma (x)+\gamma (u_{i})+\gamma (u_{i+1})+\gamma (xu_{i})+\gamma (xu_{i+1})+\gamma (u_i u_{i+1}),\\ wt_{3}&= wt_{\gamma } (yv_i w_{i+1}) = \gamma (y)+\gamma (w_{i})+\gamma (w_{i+1})+\gamma (yw_{i})+\gamma (yw_{i+1})+\gamma (v_i w_{i+1}),\\ wt_{4}&= wt_{\gamma } (zw_i w_{i+1}) = \gamma (z)+\gamma (w_{i})+\gamma (w_{i+1})+\gamma (zw_{i})+\gamma (zw_{i+1})+\gamma (w_i w_{i+1}).\\ \end{aligned}$$
The weights of \(C_{3}\odot P_m\) after calculating and summarizing are listed below for \(1\le i \le \sigma -1\):
$$\begin{aligned} wt_{1}&= 10,12,14,…,2\sigma +4,\\ wt_{2}&= 6,7,8,…,i+5,\\ wt_{3}&= 8,9,…,i+\sigma +4,\\ wt_{4}&= 11,12,…,i+2\sigma +4. \end{aligned}$$
For two arbitrary subgraphs \(C_{3}^{j+1}\) and \(C_{3}^{j}\) which have an isomorphism with \(C_{3}^{\Re (j)}\) under the labeling \(\gamma\), for \(1\le j \le t\). It is simple to verify that all weights are consecutive, such as \(wt_\gamma (C_{3}^{j}) \ne wt_\gamma (C_{3}^{j+1})\). Furthermore, \(wt_\gamma (C_{3}^{j}) – wt_\gamma (C_{3}^{j+1}) = 1\). At this point \(1 \le j \le t\) is a parameter. This concludes the proof. \(\square\)
This result provides a bound for labeling corona-style subnetworks where devices (paths) are clustered around a main cycle (core router). It shows that even as subnet sizes grow, the labeling remains manageable, which is ideal for extending LANs by adding new departments or remote clusters. Figure 5 demonstrates a total labeled graph of \(C_{3}\odot P_{36}\) with 109 isomorphic copies of \(C_{3}^{\Re (j)}\).
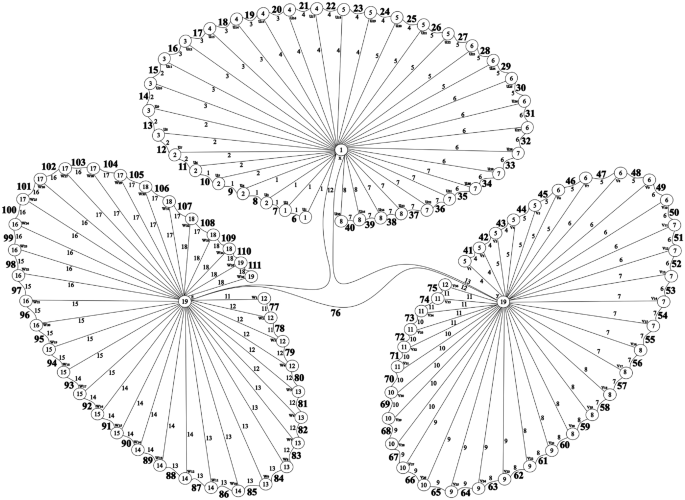
Total \(C_{3}^{\Re (j)}\)-irregular labeling of a \(C_{3}\odot P_{36}\).
Edge \(C_{3}^{\Re (j)}\)-irregularity strength of \(C_{3}\odot P_m\)
Edge-covering in \(C_{3}\odot P_m\) is the collection of subgraphs which originate a set as \(C_{3}^{\Re (j)} = C_{3}^{\Re (1)}, C_{3}^{\Re (2)},\ldots , C_{3}^{\Re (t)}\), with the condition that every edge of \(C_{3}\odot P_m\) is present in at least one subgraph \(C_{3}^{\Re (j)} \subset C_{3}\odot P_m\), here \(\Re (j)=i\) and \(j = 1, 2,\dots , t\). At that instant it is said that \(C_{3}\odot P_m\) admits a (\(C_{3}^{\Re (1)}, C_{3}^{\Re (2)},\dots , C_{3}^{\Re (t)}\))-(edge) covering. A \(C_{3}^{\Re (j)}\)-covering exists when every subgraph \(C_{3}^{\Re (j)}\) has an isomorphism to the specified subgraph \(C_{3} \subset C_{3}\odot P_m\). Every isomorphic subgraph of \(C_{3}^{\Re (j)}\) is contained in \(C_{3}^{\Re (j)}\)-covering. The associated weight of \(C_{3}^{\Re (j)}\) with edge \(C_{3}^{\Re (j)}\)-labeling \(\beta\) is stated as,
$$wt(C_{3}) = \sum _{uv\in E(C_{3}\odot P_m)} \beta (uv).$$
Here, \(\beta\) defines the edge \(C_{3}\)-labeling in \(C_{3} \odot P_m\). For two arbitrary subgraphs \(1 \le a\), \(C_{3}^{\Re (a)}\) and \(C_{3}^{\Re (a+1)}\) if the following inequality is satisfied, \(wt(C_{3}^{\Re (a)}) \ne wt(C_{3}^{\Re (a+1)}).\) then irregular \(C_{3}^{\Re (j)}\)-labeling in \(C_{3}\odot P_m\) exists. Ultimately, \(C_{3}^{\Re (j)}\)-irregularity for edges under \(C_{3}^{\Re (j)}\)-labeling is represented as \(ehs(C_{3} \odot P_m, C_{3}),\) which was proposed initially in40. Edge irregularity strength is acquired when there exists a k with \(0 \le k, k \subset Z\), for which \(ehs(C_{3}\odot P_m, C_{3})\) is achievable under \(C_{3}^{\Re (j)}\) labeling. Now, we are going to determine \(ehs(C_{3} \odot P_m, C_{3})\) for the modified structure of \(C_{3} \odot P_m\) under \(C_{3}^{\Re (j)}\)-covering with the help of Lemma 4.
Theorem 5
Let \(C_{3}\odot P_m\) be the corona product of cycle graph and path graph \(P_m\). The graph \(C_{3}\odot P_m\) is admitting \(C_{3}-covering\) generating a family of \(~3\sigma -2\) isomorphic copies of \(C_{3}^{\Re (j)}\) as \(\left( C_{3}^{\Re (1)}, C_{3}^{\Re (2)}, C_{3}^{\Re (3)},\dots , C_{3}^{\Re (3\sigma -2)}\right)\) with a parameter \(3 \le \sigma\). Then
$$\mathrm{{ehs}}(C_{3}\odot P_m, C_{3}) = \sigma$$
Proof
Let \(C_{3}\odot P_m = C_{3}\odot P_m\) be the corona product of graphs with a positive integer \(\sigma\), where \(3 \le \sigma\). Furthermore, k is the least positive integer for which \(C_{3}\odot P_m\) admits \(C_{3}^{\Re (j)}\)-irregular edge \(C_{3}^{\Re (j)}\)-labeling. Edge set for \(C_{3}\odot P_m\) is defined as:
$$E(C_{3}\odot P_m) = \{xy,yz,zx,\} \cup \{xu_i,yv_i,zw_i, u_iu_{i+1},v_iw_{i+1},w_iw_{i+1}: 1\le i \le \sigma \}.$$
From lemma 4, \(\mathrm{{ehs}}(C_{3}\odot P_m,C_{3}) \ge \sigma\). Take \(k=\sigma\) to check that k represents the upper boundary of \(\mathrm{{ehs}}(C_{3}\odot P_m,C_{3})\) with given constraints \(1 \le i \le \sigma\), \(3 \le \sigma\). Edge labeling for \(C_{3}\odot P_m\) is set up as follows:
$$\beta : E(C_{3}\odot P_m)\rightarrow \{1,2,3, \dots ,k\}.$$
\(C_{3}^{\Re (j)}\) – irregular edge labeling \(\beta\) for \(C_{3}\odot P_m\) is provided below:
$$\begin{aligned} \beta (xu_i)&= \Big \lceil \dfrac{i+1}{3}\Big \rceil , \quad { if 2\le i \le \sigma -1}\\ \beta (zw_i)&= \Big \lceil \dfrac{i+2\sigma }{3}\Big \rceil , \quad {if 2 \le i \le \sigma -1}\\ \beta (u_{i-1} u_i)&= \Big \lceil \dfrac{i}{3}\Big \rceil , \qquad {if 1 \le i \le \sigma -1}\\ \beta (xy)&= {\left\{ \begin{array}{ll} 2\Big \lceil \dfrac{ \sigma -2}{3}\Big \rceil +1,& {if \sigma \equiv 0,1 (mod 3)} \\ \\ \Big \lceil \dfrac{2\sigma +2}{3}\Big \rceil ,& {if \sigma \equiv 2 (mod 3)} \end{array}\right. } \\ \beta (yz)&= {\left\{ \begin{array}{ll} 2\Big \lceil \dfrac{ \sigma -4}{3}\Big \rceil +2,& {if \sigma \equiv 0,2 (mod 3)} \\ \\ \Big \lceil \dfrac{2\sigma +1}{3}\Big \rceil ,& {if \sigma \equiv 1 (mod 3)} \end{array}\right. } \\ \beta (zx)&= {\left\{ \begin{array}{ll} 2\Big \lceil \dfrac{ \sigma -3}{3}\Big \rceil +1,& {if \sigma \equiv 1,2 (mod 3)} \\ \\ \Big \lceil \dfrac{2\sigma }{3}\Big \rceil ,& {if \sigma \equiv 0 (mod 3)} \end{array}\right. } \\ \beta (yv_i)&= {\left\{ \begin{array}{ll} 1,\quad {if i=1, \sigma =3}\\ \Big \lceil \dfrac{i+\sigma }{3}\Big \rceil , \quad {if 2 \le i \le \sigma -1} \end{array}\right. } \\ \beta (w_{i-1} v_i)&= {\left\{ \begin{array}{ll} 2,& {if 1 \le i \le \sigma -1}\\ \Big \lceil \dfrac{i+\sigma -1}{3}\Big \rceil ,& {if 1 \le i \le \sigma -1}\\ \end{array}\right. } \\ \beta (w_{i-1} w_i)&= \Big \lceil \dfrac{i+2\sigma -1}{3}\Big \rceil , \quad {if 2\le i \le n} \end{aligned}$$
It is easily evident that all labels of edge in \(C_{3}\odot P_m\) with \(C_{3}^{\Re (j)}\)-labeling are at most k. The weight of all subgraphs in \(C_{3}\odot P_m\) generate the following results for \(1 \le i \le \sigma -1\),
$$\begin{aligned} wt_{1}&= wt_{\gamma } (xyz) = \gamma (xy)+\gamma (yz)+\gamma (zx), \\ wt_{2}&= wt_{\gamma } (xu_i u_{i+1}) = \gamma (xu_{i})+\gamma (xu_{i+1})+\gamma (u_i u_{i+1}),\\ wt_{3}&= wt_{\gamma } (yv_i w_{i+1}) = \gamma (yw_{i})+\gamma (yw_{i+1})+\gamma (v_i w_{i+1}),\\ wt_{4}&= wt_{\gamma } (zw_i w_{i+1}) = \gamma (zw_{i})+\gamma (zw_{i+1})+\gamma (w_i w_{i+1}),\\ \end{aligned}$$
The weights in \(C_{3}\odot P_m\) after computing and summarizing are provided below for \(1\le i \le \sigma -1\):
$$\begin{aligned} wt_{1}&= 7,9,11,…,2\sigma +1,\\ wt_{2}&= 3,4,5,…,i+2,\\ wt_{3}&= 5,6,7,…,i+\sigma +1,\\ wt_{4}&= 8,9,10,…,i+2\sigma +1.\\ \end{aligned}$$
It is simple to verify that for two arbitrary subgraphs, \(C_{3}^{\Re (a)}\) and \(C_{3}^{\Re (a+1)}\) for \(1\le a\) under edge labeling \(\beta\), the following connection between their weights exist. \(wt(C_{3}^{\Re (a)}) \ne wt(C_{3}^{\Re (a+1)})\). Here, \(3\le i\le \sigma -1\). We get,
$$\mathrm{{ehs}}(C_{3}\odot P_m,C_{3}) = \sigma .$$
This completes the proof. \(\square\)
In figure 6, \(C_{3}\odot P_m\) illustrates an edge irregular \(C_{3}^{\Re (j)}\)-labeling under t isomorphic copies of \(C_{3}^{\Re (j)}\), where \(0 \le t = 3\sigma -2\).
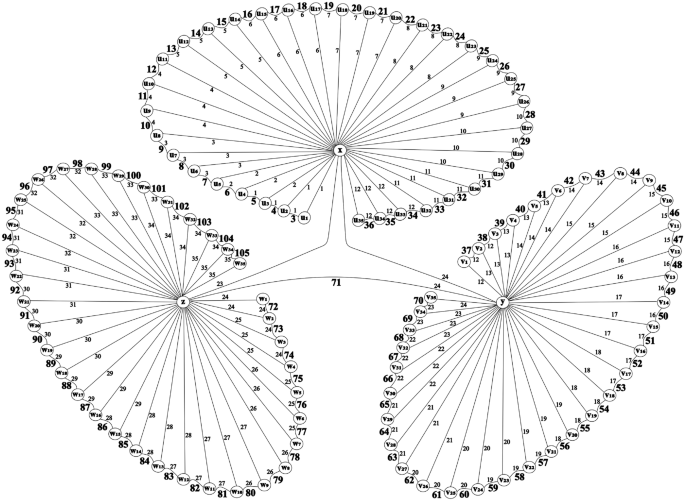
Edge \(C_{3}^{\Re (j)}\)-irregular labeling of a \(C_{3}\odot P_m\) \(= C_{3}\odot P_m (u_i, v_i, w_i)\) for a positive integer i, where \(1\le i \le 35\).
Vertex \(C_{3}^{\Re (j)}\)-irregularity strength of \(C_{3}\odot P_m\)
For vertex irregularity strength, there exist covering \(C_{3}\odot P_m\) which is described as a collection of subgraphs given by \(C_{3}^{\Re (1)}, C_{3}^{\Re (2)},\dots , C_{3}^{\Re (t)}\), on the condition that every vertex of \(C_{3}\odot P_m\) appears in at least one subgraph which is predefined in the preceding family of subgraphs \(C_{3}^{\Re (j)}\), here \(\Re (j)=j\) and \(j = 1, 2,\dots , t\). At this point, it is stated that \(C_{3}\odot P_m\) admits a (\(C_{3}^{\Re (1)}, C_{3}^{\Re (2)},\dots , C_{3}^{\Re (t)}\))-(vertex) covering. \(C_{3}^{\Re (j)}\)-covering occurs if each subgraph \(C_{3}^{\Re (j)}\) has an isomorphism corresponding to the specified subgraph. Under vertex \(C_{3}^{\Re (j)}\)-labeling \(\alpha\), the associated weight of \(C_{3}^{\Re (j)}\) is,
$$wt(C_{3}) = \sum _{u\in V(C_{3}\odot P_m)} \alpha (u).$$
Here, \(\alpha\) represents the \(C_{3}^{\Re (j)}\) vertex labeling associated with subgraph and \(C_{3}^{\Re (j)}\subseteq C_{3}\odot P_m\). If two arbitrary subgraphs \(C_{3}^{\Re (j)}\) and \(C_{3}^{\Re (j+1)}\) have an isomorphism with the provided subgraph \(C_{3}^{\Re (j)}\), the required requirements need to be proved, i.e., \(wt(C_{3}^{\Re (j)}) \ne wt(C_{3}^{\Re (j+1)})\) and their weight difference is one. This situation demonstrates vertex \(C_{3}^{\Re (j)}\)-irregular labeling in \(C_{3}\odot P_m\). For a least positive integer k if there exist irregularity in \(C_{3}\odot P_m\). under \(C_{3}^{\Re (j)}\) covering then vertex irregularity strength exist. It is written as \(vhs(C_{3}\odot P_m, C_{3}).\) Using Lemma 5, the general form of \(C_{3}\odot P_m\) for \(C_{3}^{\Re (j)}\) covering will be computed. Figure 7 illustrates a \(C_{3}^{\Re (j)}\)-irregular vertex structure of a graph.
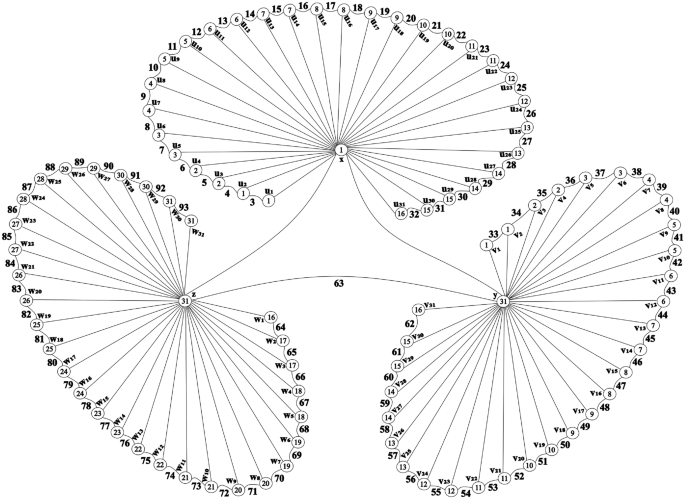
Vertex \(C_{3}^{\Re (j)}\)-irregular labeling of a \(C_{3}\odot P_m\) \(C_{3}^{184} = (u_i, v_i, w_i)\) for a positive integer i, where \(1\le i\le 60\).
Theorem 6
Let \(C_{3}\odot P_m\) be the corona product of cycle graph and path graph \(P_m\). The graph \(C_{3}\odot P_m\) is admitting \(C_{3}-covering\) generating a family of \(~3\sigma -2\) isomorphic copies of \(C_{3}^{\Re (j)}\) as \(C_{3}^{\Re (j)} = (C_{3}^{\Re (1)}, C_{3}^{\Re (2)}, C_{3}^{\Re (3)},\ldots , C_{3}^{\Re (3\sigma -2)})\) with a parameter \(3 \le \sigma\). Then
$$\mathrm{{vhs}}(C_{3}\odot P_m, C_{3}) = \sigma .$$
Proof
Assume \(C_{3}\odot P_m (u_{i}, w_{i}, w_{i})\) is the corona product of cyclic and path graphs of order 3 and m, respectively, for a positive integer \(\sigma\), for \(3 \le \sigma -1\). \(C_{3}\odot P_m\) has order \(3(m +2)\) and size \(6(m +1)\). Furthermore, k is the minimum positive integer that ensures \(C_{3}\odot P_m\) admits \(C_{3}^{\Re (j)}\)-irregular vertex labeling. The vertex set for \(C_{3}\odot P_m\) is given as,
$$V(C_{3}\odot P_m) = \{x,u,v,w\} \cup \{u_i,v_i,w_i: 1\le i \le \sigma -1 \}$$
Based on Lemma 5, \(\mathrm{{vhs}}(C_{3}\odot P_m,C_{3}) \ge \sigma\). Vertex labeling for \(C_{3}\odot P_m\) is described as
$$\alpha : V(C_{3}\odot P_m)\rightarrow \{1,2,3,\dots ,k\}.$$
\(\alpha\) for \(C_{3}\odot P_m\) with order m along with size \(m-1\), for \(1 \le i \le \sigma -1, 3\le \sigma\), as follows:
$$\begin{aligned} \alpha (u_i)&=\Big \lceil \dfrac{i}{2}\Big \rceil ,\\ \alpha (v_i)&=\Big \lceil \dfrac{i+n}{2}\Big \rceil ,\\ \alpha (w_i)&=\Big \lceil \dfrac{i}{2}\Big \rceil ,\\ \alpha (x)&=1,~~ \alpha (y)= \sigma = \alpha (z). \end{aligned}$$
It is easily evident that each of the label for vertices in \(C_{3}\odot P_m\) with \(C_{3}^{\Re (j)}\)-labeling are limited to k. The weight of t isomorphic subgraphs in \(C_{3}\odot P_m\) leads to the following relations:
$$\begin{aligned} wt_{1}&= wt (xyz) = \alpha (x)+\alpha (y)+\alpha (z),&\\ wt_{2}&= wt (xu_i u_{i+1}) = \alpha (x)+\alpha (u_{i})+\alpha ( u_{i+1}),&{if 1\le i \le \sigma -1},\\ wt_{3}&= wt (yv_i w_{i+1}) = \alpha (y)+\alpha (w_{i})+\alpha ( w_{i+1}),&{if 1\le i \le \sigma -1},\\ wt_{4}&= wt (zw_i w_{i+1}) = \alpha (z)+\alpha (w_{i})+\alpha ( w_{i+1}),&{if 1\le i \le \sigma -1}. \end{aligned}$$
The weights for the mathematical model of \(C_{3}\odot P_m\) after simplifying are provided below for \(1\le i \le \sigma -1\),
$$\begin{aligned} wt_{1}&= 7,9,11,…,2\sigma +1,\\ wt_{2}&= 3,4,5,…,i+2,\\ wt_{3}&= 5,6,7,…,i+\sigma +1,\\ wt_{4}&= 8,9,10,…,i+2\sigma +1.\\ \end{aligned}$$
Any two arbitrary subgraphs \(C_{3}^{\Re (a)}\) and \(C_{3}^{\Re (a+1)}\) for \(1\le a \le j\) are isomorphic to \(C_{3}^{\Re (j)}\) under the labeling \(\alpha\). It is simple to check that \(wt(C_{3}^{\Re (a)}) \ne wt_(C_{3}^{\Re (a+1)})\) and \(wt_(C_{3}^{\Re (a)}) – wt_(C_{3}^{\Re (a+1)}) = 1\). In this case, \(s\ge 1\), and \(3\le j \le \sigma -1\) represents the \(C_{3}^{\Re (j)}\) labeling parameter. It concludes the proof. \(\square\)
link








